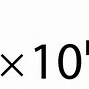
Aturan Angka Penting Dalam Perkalian

Tabel Perkalian 1-10 dan Cara agar Cepat Menghafal Perkalian

2. Rendy ingin membuatkan plat nomor kendaraan yang terdiri dari 4 angka yang dipilih dari angka-angka 1, 2, 3, 4, 5 dan dalam plat nomor itu boleh ada angka yang sama. Berapa banyak plat nomor dapat dibuat?

Tabel Perkalian 1 Sampai 10, Permudah sang Buah Hati Belajar Matematika

Adapun lima contoh soal aturan perkalian dan jawabannya, yang dilansir iNews.id dari berbagai sumber, Kamis (22/2/2024), adalah sebagai berikut.

Aturan Perhitungan Angka Penting

Berikut ketentuan perhitungan angka penting pada penjumlahan, pengurangan, perkalian, pembagian, pangkat, dan akar:

Contoh Soal Kombinasi

Sebuah maskapai pesawat baru memiliki 5 pesawat terbang. 2 dari 5 pesawat tersebut memiliki jadwal penerbangan ke Pulau Lombok.

Hitunglah berapa cara yang bisa tercipta untuk memilih pesawat dari maskapai tersebut!

5C2 = 5! / (2! (5 – 2)!

5C2 = 5 x 4 x 3 x 2 x 1 / ((2 x 1) (3 x 2 x1))

5C2 = ( 5 x 4) / ( 2 x 1)

Jadi, ada 10 cara yang bisa dilakukan untuk memilih pesawat untuk penerbangan ke Pulau Lombok.

Sebuah toko online menjual 10 jenis kue lebaran. Vivian berniat untuk membeli 5 toples. Dari 10 jenis kue lebaran tersebut, Vivian sudah menentukan ingin membeli 3 jenis saja.

Tentukan berapa banyak kombinasi kue lebaran yang bisa dibeli Vivian!

Fakta bahwa Viaian telah menentukan 3 jenis kue lebaran, maka tersisa 5 toples slot kue lebaran yang akan dipilih olehnya.

Selain itu, ada juga 7 pilihan jenis yang bisa menjadi pilihan Vivian. Dari keterangan tersebut, berikut ini cara pengerjaannya:

7C5 = 7! / (5! (7-5)!)

7C5 = ( 7 x 6 x 5 x 4 x 3 x 2 x 1) / (( 5 x 4 x 3 x 2 x 1 ) ( 2 x 1 ))

7C5 = ( 7 x 6) / ( 2 x 1 )

Jadi, dari 5 toples kue lebaran yang dibeli oleh Vivian bisa ada 21 variasi.

Demikianlah contoh soal aturan penjumlahan, perkalian, permutasi, dan kombinasi bagian terakhir.

Contoh Soal PAS Matematika Kelas 7 Semester 1 Terbaru 2024 beserta Jawabannya Lengkap

Kalkulator Angka Penting

Kalkulator Angka Penting ini menghitung jumlah angka penting, atau digit, yang berisi suatu angka dan menampilkan angka mana yang signifikan.

Angka atau digit yang signifikan adalah nilai dalam sebuah angka yang dapat diandalkan agar akurat. Bilangan signifikan dalam suatu bilangan adalah nilai yang dapat ditentukan dengan pasti atau tingkat keyakinan yang tinggi agar akurat, sedangkan angka yang tidak signifikan adalah angka yang kami anggap tidak akurat.

Bilangan signifikansi banyak digunakan selama pengukuran. Pengukur yang berbeda dapat merekam pengukuran dengan akurasi berbeda. Beberapa alat ukur dapat merekam jauh lebih detail dibandingkan alat ukur lainnya. Misalnya, jika kita memiliki penggaris yang hanya mengukur sentimeter, kita dapat mengukur hingga seperseratus meter. Jika sekarang kita mengubah penggaris dan memiliki pengukuran dalam milimeter, kita dapat mengukur hingga seperseribu meter. Dengan demikian, kita dapat memiliki digit ekstra signifikan, karena penggaris lebih detail dan memungkinkan pengukuran yang lebih akurat.

Penting untuk jujur saat melakukan pengukuran, agar nilai resulant tidak terlihat lebih akurat dari peralatan yang digunakan untuk melakukan pengukuran. Dan cara kami membuat nilai yang terekam menjadi jujur adalah dengan mengontrol jumlah digit, atau angka signifikan, yang digunakan untuk melaporkan pengukuran. Nilai yang tercatat tidak boleh lebih signifikan dari yang dimungkinkan oleh alat ukur.

Jadi, misalnya jika kita melakukan pengukuran dan kita dapat menyatakan nilainya sebagai 230 gram. Angka 2 dan 3 adalah angka penting, sedangkan angka 0 bukan. Angka 0 tidak pasti karena kami tidak percaya itu akurat. Jadi, untuk angka 230, hanya 2 dan 3 yang kita ketahui dengan tingkat akurasi yang tinggi, sedangkan 0 tidak pasti dan tidak dapat dipercaya. Jadi, angka 230 hanya memiliki 2 angka penting.

Misalnya, timbangan perangko mengukur dalam gram. Itu tidak dapat mengukur sepersepuluh gram, seperseratus gram, dll., Hanya dari satu gram. Pengukuran dalam gram +/- 1 gram hanya dapat dilakukan. Oleh karena itu, hanya dapat mengukur keakuratan 1 digit signifikan. Namun, timbangan dua panci dapat mengukur hingga seperseratus gram. Oleh karena itu, ia akan memiliki 3 digit signifikan, satu untuk tempat satuan, satu untuk tempat kesepuluh, dan satu untuk tempat keseratus. Timbangan analitik dapat mengukur hingga seperseribu gram, sehingga dapat memiliki hingga 4 digit signifikan.

Dengan semua alat ukur yang dibahas di atas, angka signifikansi yang benar harus dipatuhi. Bayangkan jika sebuah alat pengukur hanya dapat mengukur seperseratus gram seperti keseimbangan dua panci dan kita mengatakan bahwa alat itu mencatat pengukuran hingga seperseribu gram. Ini akan membuat hasil kami sangat mencurigakan dan tidak akurat. Jika sebuah alat dapat mengukur hanya seperseratus gram, bagaimana Anda bisa mendapatkan nilai seakurat seperseribu gram. Oleh karena itu, tokoh penting bisa menjadi sangat penting dalam komunitas ilmiah. Ini menunjukkan seberapa akurat sebuah angka, berdasarkan jumlah digit signifikan yang ada dalam nomor tersebut.

Sekarang setelah Anda mengetahui pentingnya angka penting, mari kita bahas aturan untuk memutuskan angka mana yang signifikan dan mana yang tidak signifikan.

∙ Semua angka bukan nol adalah signifikan. Contoh: 5,4789- Semua digit bukan nol. Oleh karena itu, semua digit signifikan. Jadi, memiliki 5 digit signifikan.

∙ Angka nol antara angka bukan nol signifikan. Contoh: 2,00008- Semua angka nol dalam angka ini signifikan. Oleh karena itu, memiliki 6 digit signifikan.

∙ Nol di akhir angka signifikan jika angka tersebut berisi desimal. Contoh: 45,00- Angka nol dalam angka ini signifikan. Oleh karena itu, memiliki 4 digit signifikan.

∙ Nol di akhir angka signifikan jika ada koma desimal. Contoh: 12.000.- Angka nol dalam angka ini signifikan. Oleh karena itu, memiliki 5 digit signifikan.

∙ Nol di akhir angka tidak signifikan jika angka tersebut tidak mengandung titik desimal. Contoh: 3.400- Angka nol dalam angka ini tidak signifikan. Oleh karena itu, memiliki 2 digit signifikan.

∙ Nol di sebelah kiri digit bukan nol pertama setelah titik desimal tidak signifikan. Contoh: 0,000076- Angka nol pada gambar ini tidak signifikan. Oleh karena itu, memiliki 2 digit signifikan.

∙ Angka nol setelah digit bukan nol pertama setelah desimal adalah signifikan. Contoh: 0,0005600- 3 angka nol pertama tidak signifikan. 2 angka nol terakhir adalah. Oleh karena itu, angka ini memiliki 4 digit signifikan.

Ini adalah aturan umum untuk mengetahui angka mana yang signifikan dan mana yang tidak.

Untuk menggunakan kalkulator ini, pengguna cukup memasukkan angka. Setelah nomor dimasukkan, pengguna mengklik tombol 'Temukan Jumlah Angka Penting'. Angka signifikan yang dihasilkan akan dihitung secara otomatis.

Karena elektronik, seperti sains lainnya, berkaitan dengan pengukuran, penting untuk mengetahui cara menangani bilangan signifikan. Alat ukur menentukan seberapa akurat pengukurannya. Mungkin sangat penting menggunakan angka-angka penting yang benar, untuk alasan-alasan yang dibahas di atas.

Kalkulator Pembulatan Angka Penting Kalkulator Notasi Ilmiah Kalkulator Pengujian Hipotesis

Contoh Soal Aturan Penjumlahan, Perkalian, Permutasi, dan Kombinasi beserta Pembahasannya – Mendekati ulangan harian atau ujian, cara terbaik untuk belajar lebih efektif adalah dengan mengerjakan contoh soal.

Bila kamu sedang mencari contoh soal aturan penjumlahan, perkalian, permutasi, dan kombinasi; maka kamu berada di halaman yang tepat! Lanjut baca hingga akhir, ya!

Cara Menghitung Penjumlahan, Pengurangan, Perkalian, Pembagian dalam Bentuk Pecahan

- Banyak sepatu yang dimiliki Tasya ada 2. Tasya dapat memilih salah satu dari 2 sepatu tersebut.

Oleh karena Tasyaharus memakai keduanya yaitu tas dan sepatu, banyak pilihan yang dimiliki Rani adalah 3 × 2 = 6.

Contoh Soal Permutasi

Sebuah kaleng bekas biskuit dijadikan tempat beberapa warna benang jahit.

Jumlahnya ada 7 benang jahit dengan warna yang berbeda-beda. 3 benang berwarna hitam, 2 benang berwarna merah, dan 2 benang berwarna putih.

Bila gulungan benang tersebut secara teratur disusun sebaris, tentukanlah berapa banyak variasi susunan yang bisa tercipta!

P = 7 x 6 x 5 x 4 x 3 x 2 x 1 / ( 3 x 2 x 1 ) ( 2 x 1 ) ( 2 x 1 )

P = 7 x 6 x 5 x 4 / 4

Jadi, variasi susunan yang bisa tercipta dari 7 benang berbeda warna adalah 210 variasi.

Sebuah organisasi baru saja terbentuk dan ingin membuat susunan kepengurusan.

Diketahui jumlah anggota saat ini ada sebanyak 10 anggota. Posisi yang dibutuhkan adalah ketua, wakil, bendahara, sekretaris, dan pengawas.

Dari data tersebut, tentukanlah berapa peluang variasi dari susunan panitia yang bisa tercipta!

10P5 = 10! / ( 10 – 5 )!

10P5 = (10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) / (5 x 4 x 3 x 2 x 1)

10P5 = 10 x 9 x 8 x 7 x 6

Jadi, jumlah variasi dari susunan pengurus yang bisa tercipta adalah 30240.

Sebuah presentasi akan dilakukan dan masing-masing kelompok berjumlah 4 orang. Tentukan berapa variasi dari tempat duduk yang bisa dibuat!

Jadi, jumlah variasi tempat duduk yang bisa tercipta adalah 6.

Itulah bagian ketiga dari contoh soal aturan penjumlahan, perkalian, permutasi, dan kombinasi. Yuk, lanjut pelajari bagian contoh soal kombinasi di bawah!

Contoh Soal Penalaran Matematika Persiapan SNBT 2023 Beserta Jawabannya

Penjumlahan dan Pengurangan

Angka hasil penjumlahan atau pengurangan hanya boleh dituliskan satu angka taksiran. Misalnya, hasil penjumlahan 3,219 cm; 15,5 cm; dan 8,43 cm adalah 27,149 cm. Maka, hasil akhirnya harus dituliskan menjadi 27,1 cm, sehingga hanya memiliki satu angka taksiran.

Setiap angka bukan nol adalah angka penting

Aturan angka penting yang pertama adalah setiap angka yang bukan nol adalah angka penting.

Misalnya, bilangan 1.234 memiliki 4 angka penting yaitu 1, 2, 3, dan 4.

Setiap angka nol di antara angka bukan nol adalah angka penting

Angka penting selanjutnya adalah angka nol yang berada di antara dua angka bukan nol.

Misalnya, bilangan 201 yang 0-nya merupakan angka penting karena berada di antara angka 2 dan 1.

Baca juga: Macam-Macam Bilangan dan Pengertiannya

Perkalian dan Pembagian

Penulisan jumlah angka penting hasil perkalian atau pembagian sama dengan jumlah angka penting paling sedikit dari bilangan-bilangan yang dioperasikan. Misalnya, hasil perkalian antara 1,6283 cm (4 angka penting) dengan 2,2 cm (2 angka penting) adalah 1,8226 cm. Maka, hasil akhirnya harus dituliskan menjadi 1,8 cm (2 angka penting).

Sementara itu, perkalian angka antara hasil pengukuran dengan hasil membilang, hasil akhirnya harus mempunyai jumlah angka penting paling sedikit yang sama dengan angka penting pada hasil pengukuran.

Misalnya, keramik lantai mempunyai panjang 50,25 cm dan lebar 20,1 cm (panjang dan lebar adalah angka dari hasil pengukuran). Apabila terdapat 25 buah keramik (jumlah angka dari hasil membilang) yang digunakan untuk menutup lantai, maka berapakah luas lantai yang tertutup keramik?

-   Panjang = 50,25 cm (4 angka penting), lebar = 20,1 cm (3 angka penting), dan jumlah keramik = 25 keramik (dua angka penting).

-   Untuk mengukur luas lantai = panjang x lebar x jumlah keramik = 50,25 x 20,1 x 25 = 25.250,625 cm2.

-   Maka, hasil akhirnya harus ditulis 25.200 atau 2,52 x 104 cm2 (3 angka penting).

Dalam menuliskan angka penting tersebut berlaku aturan pembulatan angka 5. Jika sebelum angka 5 terdapat bilangan ganjil, maka dibulatkan ke atas. Sementara apabila sebelum angka 5 terdapat bilangan genap, maka angka 5 dihilangkan. Misalnya, 2,25 menjadi 2,2 dan 2,35 menjadi 2,4.

Jumlah angka penting dari hasil perhitungan pangkat atau akar harus mempunyai jumlah angka penting yang sama dengan yang dioperasikan. Misalnya:

-   Akar dari 2,25 adalah 1,5, lalu ditulis menjadi 1,50.

-   Pangkat dua dari 2,5 adalah 6,25, lalu ditulis menjadi 6,2 (berlaku aturan pembulatan angka 5).

KOMPAS.com – Dalam suatu bilangan, tidak semua angka merupakan angka penting. Apa yang dimaksud dengan angka penting? Berikut adalah pengertian, aturan, dan contohnya!